1.引言

鋁合金在擠壓成形過程中，由于受到擠壓筒壁、模具端面、分流孔、焊合腔、工作帶表面等部位的劇烈摩擦，各位置的流速是極不均勻的。當擠壓形狀不對稱，各部分尺寸，形狀相差很大的制品時，這種流動不均勻性更會顯著增加。而且，在模具設計制造中，各部位流動速度的差異不可能完全的消除或調整。因此，擠壓成形中，不能避免的會產生各種成形缺陷，如扭擰、彎曲、波浪、裂紋等^[1]。擠壓模具在使用中，鋁型材不成形、波浪、彎曲等由于金屬擠出模孔速度不均勻引起的試模不合格，是造成試模不合格的主要原因之一。為了消除以上這些缺陷，最理想的結果就是金屬在擠出模孔時，各個部位各個質點的金屬流動速度均保持一致。而實際的情況是，金屬在擠出模孔時，即使最簡單的鋁型材也不可能各個質點都獲得相同的流動速度。因此，必然存在一個速度差異范圍，當金屬擠出模孔時，當各個質點的擠出速度差異在這一個范圍之內時，擠出的鋁型材能夠穩定成形。

2.穩定成形機理分析

根據最基本的金屬塑性成形原理，金屬在塑性變形時，總是向著變形阻力最小的方向流動。因此，金屬的應力狀態是影響金屬流動變形的根本因素。在擠壓成形出材的過程中，常見的一些成形缺陷，如波浪、扭擰、側彎等，形成的根本原因是擠出的金屬的應力負載超過了保持其原來穩定狀態的臨界應力，從而使擠出金屬發生彎曲、皺曲、扭轉等變形。

對于擠出模孔的金屬，一般情況下，只受到模孔出口截面的約束作用，在其它方向、位置上均處于自由狀態（忽略了與擠壓方向垂直的重力作用和擠壓牽引設備的支撐力作用），如圖1所示。而在離模孔出口足夠遠的位置，金屬的塑性成形已經完成，因此，考察擠壓成形出材的穩定性，只需對從模孔出口以外的一小段進行考察。

以簡單的扁條鋁型材為例，對擠出模孔的金屬進行受力分析。對于擠壓成形的鋁型材而言，鋁型材的壁厚相比各鋁型材壁面一般較小，可看作為薄板。

若金屬擠出模孔各位置的軸向速度完全一致，即v_xi v_out，且v_yi0  (1)

則擠出部分的金屬各部位的流動應力相等，金屬不發生變形。

    若金屬擠出模孔各位置的速度不完全相等，假設中心位置的金屬擠出較快，假設BC段的速度為v₁，邊緣位置的金屬流動速度較慢，AB、CD段的速度為v₂, 有v₁ > v₂，如圖2(1)所示。在一個很短的時間Δt后，BC段沿著擠壓方向向前運動了v₁ Δt，到達B'C'，而AB、CD段則沿著擠壓方向向前運動了v₂Δt，到達A'B''和C''D'位置。如圖2(2)所示。

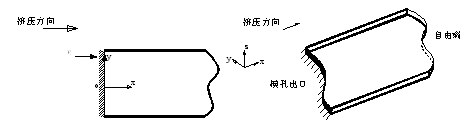
a) 水平視圖                                 b)軸側視圖

圖1 擠出模孔金屬

Fig. 1 Extruded metal

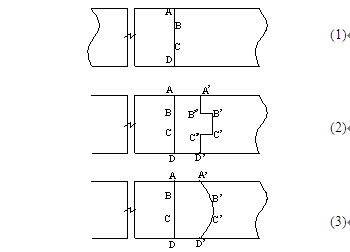
圖2 出材成形原理

Fig. 2 Principle of extrudate deformation

又根據金屬塑性變形的連續性條件，B'點和B''點應該是同一個點。而在圖2(2)的變形過程中，B'C'段比A'B''段和C''D'段多向前運動了B'B''的距離。因此，在金屬擠出模孔經過時間Δt后，“伸長”較多的BC段金屬將受到其前方已擠出金屬的擠壓應力σ_p，從而限制了擠出較快的位置金屬的擠出；而“伸長”較少的AB、CD段則受到已擠出金屬拉伸的應力σ_d，促進擠出較慢位置的金屬的擠出，從而使快慢兩部分的金屬維持相同的速度擠出，保證金屬整體上的擠出變形連續，如圖2(3)所示。

在出口位置擠出模孔較快的壁面上，金屬受到壓應力的作用；而擠出模孔較慢的壁面上，金屬則受到拉應力的作用。又由于金屬的變形和負載都是連續的，在“快”和“慢”之間，必然有一個臨界于“快”、“慢”之間的位置，即圖2(3)中的BB'連線和CC'連線的位置上，金屬既不受拉亦不受壓。在F. Halvorsen和T. Aukrust的研究^[2]當中，分析了薄板鋁型材擠出后各位置的金屬流動速度分布。得到了其分布規律符合A+Be^-C的形式。如圖3所示（圖中，x軸表示鋁型材截面上某點到中心軸線的距離，y軸是對應該點的速度），再定義：

Δv_c v­_max- v_mid         (2)

Δv_t v­_mid- v_min      (3)

Δv_λ Δv_c(1- e^-1)     (4)

  (5)

其中，v_max為出口截面的最大速度，v_mid為壁面上應力載荷為0的臨界面上金屬的擠出速度，λ為距離最大速度位置的特征值，定義特征應變速率^[2]，

        (6)

x為相應點到鋁型材中心位置的距離。圖3的實線為數值模擬獲得的曲線，而虛線為對應的式(5)指數函數的分布曲線，兩者有較好的吻合。

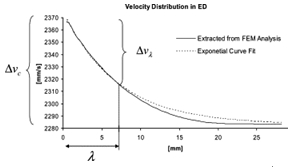
圖3 薄板鋁型材擠出方向的速度分布^[2]

Fig. 3 Plot of the velocity distribution in the extrusion direction along the symmetry plane

3.塑性屈曲問題

板殼的理論當中，經典的穩定性定義^[137,138]是在外載不變的情況下，若經過一個微小的擾動，結構從一個平衡狀態轉到另一個相鄰的平衡狀態，則原來的平衡狀態是不穩定的。若擾動除掉后結構仍能夠回到它原來的平衡狀態，則這種平衡狀態是穩定平衡的。

對于高溫下鋁合金擠壓成形出材失穩的問題屬于板的塑性屈曲問題。板的塑性屈曲遠比彈性屈曲復雜，它必須考慮非線性的物理關系^[4]。對于板的塑性屈曲這樣的非保守問題，一般只能采用動力準則對屈曲進行判定，即在有限n維空間內建立某力學系統的動力平衡方程，以u_i(i=1,2,…,n)為系統廣義的位移，為相應的廣義速度。若對于廣義位移和廣義速度在某幅度范圍內的任意初始值，求解初值問題得到的所有時刻下的和都小于某指定的值和，則系統是平衡穩定的^[3]。然而動力準則在應用上仍有許多重大問題有待于解決，因此，往往仍是通過在彈性屈曲臨界應力載荷上添加折減系數等方法進行處理。在本文的分析中，以式(7)的臨界應力估算式作為屈曲載荷的判定公式。

          (7)

其中，k為臨界應力系數，η為塑性折減系數，β為鋁型材的形狀系數，E為材料的彈性模量，μ為材料的泊松比，t為鋁型材壁板的壁厚，b為鋁型材壁板受壓區域的寬度。

根據前面的分析，鋁型材壁板受壓區域的寬度b與鋁型材壁板的寬度L是兩個不同參數。在擠壓出材壁板的截面上，既存在受壓的區域同時也存在受拉的區域。而受壓區域的寬度b與鋁型材壁板的寬度L以及出口截面的速度均勻程度的分布情況有關。在其它因素相同的情況下，b隨著L的增大而增大。由于受壓區域的寬度b在實際擠壓過程中無法測量，故式(7)難以進行應用和對比，而b與鋁型材壁板的寬度L之間近似的具有線性關系，因此近似的認為一個壁面上受壓和受拉的區域各占50%，則有 b=L/2。由此可見，當鋁型材的壁厚越小，對應位置的壁面越寬時，鋁型材產生皺曲、波浪等缺陷的可能性越大。

式(7)中的鋁型材形狀系數β與鋁型材截面的復雜程度有關，鋁型材截面交錯的壁面越多，則不同壁面之間相互的約束越大，某一壁面產生皺曲需要的臨界載荷則越大。因此，對于簡單的薄板壁面，β = 1。而對于一般的常見鋁型材，β在1.3~1.6之間取值；對于復雜截面的鋁型材，β可取到2~2.5。

又對于圖2薄板鋁型材出口初始位置的ABCD面，擠出速度的快慢是由擠壓模具的結構因素等決定的，即ABCD面的速度大小分布是穩定的。而擠出速度場的快慢差異越大，BB'和CC'之間金屬的擠出量將越來越多，BC段金屬維持原來的穩定的擠出形成的壓應力σ_p越來越大，同樣AB、CD段的拉應力σ_d也越來越大。因此，由于速度差異引起的鋁型材壁面上的應力最大值若仍小于鋁型材各壁面的穩定臨界載荷σ_critical，則鋁型材保持穩定成形。若其應力最大值超過了臨界載荷σ_critical，則在應力場超過臨界載荷的鋁型材壁面，可能發生失穩的現象，即產生波浪、彎曲的缺陷。而對于薄板構件的穩定性問題，結構中的壓應力是影響構件穩定性的主要因素，構件中的拉應力往往不會引起系統的失穩、皺曲。因此，擠出鋁型材穩定的條件應表述為：

σ_pmax ≤ σ_critical         (8)

綜合式(7)、式(8)，可以發現鋁型材薄板的屈曲與鋁型材的壁厚t、鋁型材壁面的寬度L有密切的關系。鋁型材的壁厚t越大，鋁型材壁面的寬度L越小時，對應壁面的穩定臨界載荷越大。

4.結論

在F. Halvorsen和T. Aukrust對擠壓成形屈曲產生機理的研究上進行了更深一步的研究，結合塑性屈曲理論，以臨界應力估算式作為屈曲載荷的判定公式，提出了擠出鋁型材穩定的條件。鋁型材的壁厚t越大，鋁型材壁面的寬度L越小時，對應壁面的穩定臨界載荷越大。(1) 結構中的壓應力是影響構件穩定性的主要因素，構件中的拉應力往往不會引起系統的失穩、皺曲。

(2) 鋁型材薄板的屈曲與鋁型材的壁厚t、鋁型材壁面的寬度L有密切的關系。鋁型材的壁厚t越大，鋁型材壁面的寬度L越小時，對應壁面的穩定臨界載荷越大。