我國既是鋁土礦資源豐富的大國,也是需鋁量較多的國家之一。目前,鋁已成為我國僅次于鋼鐵的第二主要金屬,占有色金飽和總產量的40%以上。堆積型鋁土礦是我國華南地區生產金屬鋁的主要來源,其礦石在冶煉前一般須先關往洗礦廠進行洗礦和配礦,以保證礦石具有較合適而穩定的鋁硅比(Al2O3品位與SiO2品位的比值)。隨著開采的不斷進行,一些堆積型鋁土礦山面臨著資源接替,如何綜合規劃已探明的新資源和即將開采完的老資源,實現采場與洗礦廠的合理匹配,從而達到盡可能多地利用低品位礦石,延長礦山服務年限的目的,成為這些礦山企業急需解決的難題。本研究運用現代物流規劃、運籌學和系統工程思想,將洗礦廠廠址與配礦方案從宏觀上統一起來,建立了混合整數的優化模型,并在某實際堆積型鋁土礦山進行了成功應用。
一、問題的抽象
設某堆積型鋁土礦有n個開采單元,第i個開采單元的保有原礦石量為Ci,礦山的服務年限為N;m個備選洗礦廠位置,第j個位置記為Xj,在此建洗礦廠的費用為Fj,洗礦廠建成后的原礦年處理能力為qj,每年由第i個開采單元運來的原礦量為Cij,相應的洗后凈礦石的量為C′ij(凈出礦率為hi)、Al2O3和SiO2的品位為Aj和Sj,來自所有開采單元的凈礦石在該洗礦廠的配礦堆場經過破碎、配礦后送往冶煉廠的成品礦年產量為Pj、鋁硅比在K1與K2之間;各洗礦廠合計每年處理的原礦石總量為Q1,洗礦后的凈礦石總量為Q2;第i個開采單元與Xj間的距離為Dij,Xj與冶煉廠間的距離為Dj;卡車的單位運輸成本為a。鋁土礦產品的產出過程如圖1所示。

圖1 堆積型鋁土礦產品產出過程
現在的問題是:應該修建哪些洗礦廠以及如何合理安排各個采場和洗礦廠的年產計劃,才能在保證送往冶煉廠的鋁土礦產品的鋁硅比達到設計要求的前提下,使建廠投資和運輸費用最小。
二、洗礦廠址和配礦方案綜合優化數學模型
如前所述,研究的核心是在保證配礦產品的鋁硅比達到設計標準的前提下,確定合適的洗礦廠個數和位置,從而達到洗礦廠建廠投資和和平運輸費用最小的目的。
從采場采出的原礦石價值很低,如果洗礦廠離采場太遠,將導致原礦石在洗礦廠的運費過高而使洗礦廠的產品喪失增值空間,因此,須對第i個開采單元與備選洗礦廠位置Xj間的距離Dij加以限制,并將Xj設置為取決于Dij的開關變量,當Dij不超限時Xj中選而賦值為1,當Dij超限時Xj落選而賦值為0,以解決洗礦廠的個數和位置問題;另外,可以通過對配礦后礦石的鋁硅比實行上、下限約束,合理搭配貧富礦石,使貧礦石得到最大限度的利用,同時確保從各個配礦堆場輸出的礦石均滿足冶煉廠對鋁硅比的要求。
根據第1節的假設和以上思路,可以得出某堆積型鋁土礦山在服務期內建洗礦廠和生產運輸的總費用為
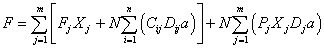
相應的約束條件為:
(一)第i個開采單元在礦山服務期內采出的原礦總量
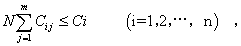
(二)第i個開采單元到第j個備選洗礦廠的卡車運輸距離
Dij≤L,
(三)第j個備選洗礦廠位置的賦值
Xj=1(中選)或0(落選)(j=1,2,…,m),
(四)第j個洗礦廠年處理原礦量
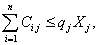
(五)第j個洗礦廠對來自第i個開采單元的原礦進行洗礦的凈出礦率
hi=(C′ij/Cij)×100%,
(六)第j個洗礦廠的配礦堆場送往冶煉廠的成品礦年產量
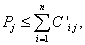
(七)第j個洗礦廠的配礦堆場配出成品礦的鋁硅比
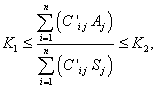
(八)m個洗礦廠年處理礦石總量
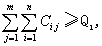
(九)m個配礦場年處理礦石總量
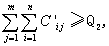
如此,按洗礦廠建廠投資和生產運輸費用最小原則,即可建立堆積型鋁土礦洗礦廠廠址和配礦方案的綜合優化數學模型為

三、應用實例
某實際堆積型鋁土礦共有42個開采單元、3個備選洗礦廠。各開采單元的存礦量及與各備選洗礦廠間的距離如表1所示,各備選洗礦廠的設計處理能力和建廠費用如表2所示。
表1 各開采單元存礦量及與備選洗礦廠間的距離
|
開采單
無序號
|
保有原礦量/萬t
|
洗后總凈礦量/萬t
|
洗后礦品位/%
|
到備選洗礦廠運距/(10-3km)
|
|||
|
Al2O3
|
SiO2
|
到X1
|
到X2
|
到X3
|
|||
|
1
2
┆
42
|
4.6740
67.1659
┆
8.7459
|
1.86960
26.86636
┆
3.49836
|
86.26
84.28
┆
81.08
|
9.20
11.28
┆
14.65
|
4350.180
3492.979
┆
9570.024
|
7865.217
7008.016
┆
6532.396
|
1504.898
8598.146
┆
5084.180
|
|
合計
|
2750.2950
|
1100.11800
|
|||||
表2 備選洗礦廠設計年處理能力和建廠費用
|
備選洗礦廠位置
|
X1
|
X2
|
X3
|
|
年處理能力qj/萬t
建廠費用Fj/萬元
|
90
20000
|
105
21300
|
95
20950
|
該礦山設計服務年限為11a,洗礦廠處理原礦石的任務總量Q1為250萬t/a、產出洗后礦的任務總量Q2為100萬t/a、配礦產品的綜合鋁硅比為10±0.5,卡車的單位運輸成本a為1.2萬元/(萬t·km),卡車從開采單元到洗礦廠的單次運輸距離上限L為11km,位于X1、X2、X3處的3個備選洗礦廠到冶煉廠的距離分別為34.7km、34.8km、3km,要求確定洗礦廠的個數和位置,并合理安排各開采單元和洗礦廠的年生產計劃,使洗礦廠建廠投資和生產運輸費用最小,同時保證各洗礦廠配礦產品的鋁硅比達到設計要求。
將已知條件代入堆積型鋁土礦洗礦廠廠址和配礦方案綜合優化數學模型,運用Dash Optimization 軟件編程求解,結果如表3所示。
表3 計算結果
|
變量名
|
值
|
變量名
|
值
|
變量名
|
值
|
變量名
|
值
|
|
minF
Q1
Q2
X1
X2
X3
C(1,1)
C(2,1)
C(3,1)
C(4,1)
C(5,1)
C(6,1)
|
875357
250
100
1
0
0
0.4249
6.106
8.6785
6.7920
12.5719
4.415.3
|
C(7,1)
C(8,1)
C(9,1)
C(10,1)
C(11,1)
C(12,1)
C(13,1)
C(14,1)
C(15,1)
C(16,1)
C(17,1)
C(18,1)
|
13.9644
3.5108
6.5542
16.3778
7.0202
7.8822
24.3702
6.1299
10.6006
10.5779
3.1672
5.8375
|
C(19,1)
C(20,1)
C(21,1)
C(22,1)
C(23,1)
C(24,1)
C(25,1)
C(26,1)
C(27,1)
C(28,1)
C(29,1)
C(30,1)
|
3.7922
4.1683
21.7519
1.8961
2.0356
1.4621
2.9068
0.1910
0.0351
0.0937
0.9400
5.1418
|
C(31,1)
C(32,1)
C(33,1)
C(34,1)
C(35,1)
C(36,1)
C(37,1)
C(38,1)
C(39,1)
C(40,1)
C(41,1)
C(42,1)
|
0.6911
4.9106
8.6051
9.5356
3.8387
0.2523
2.3108
18.7689
0.1109
0.7848
0.7951
0.6911
|
注:C(i,1)表示Cil。
由表3可知:在礦山整個服務期間,只需要建立位于X1處的1個洗礦廠即可,建廠和生產運輸總費用為875357萬元;第i個開采單元運往該洗礦廠的計劃年原礦量為C(i,1);該洗礦廠用于配礦的洗后礦計劃年產出量為100萬t。此方案已經在某實際堆積型鋁土礦的前期生產中得到了成功應用。
四、結論
對于一些面臨資源接替的堆積型鋁土礦山而言,在確保配礦產品的鋁硅比滿足設計要求的前提下,盡可能地延長礦山服務年限和獲得最大的經濟效益是其共同目標。本研究借助于現代物流規劃、運籌學等理論,結合礦山生產實踐經驗,建立了堆積型鋁土礦洗礦廠廠址和配礦方案的綜合優化數學模型,達到了如下目的:
(一)在資源儲量及分布已知的情況下,確定了洗礦廠的位置和個數,實現了采場與洗礦廠之間的合理匹配。
(二)通過對不同品位的礦石進行合理調配,既實現了貧富礦兼采,降低了生產成本,延長了礦山服務年限,又保證了配礦產品的鋁硅比滿足要求。
(三)本模型的約束條件較為普遍,礦山企業可以根據實際生產情況靈活調整年作業計劃,從而達到費用最省的目的。
(四)通過對約束條件進地增減,本模型的應用范圍可以擴展。



